
几何学与微观力学
1.微观几何
近年来,微观力学引起了学者们的关注。有不同的名称,有的称为纳米力学,有的称为细观力学,有的直接称为微观力学。但总的来说,研究的是小物体的力学。这可能是由于近期微机械制造、材料强度微裂纹研究等需求刺激所致。
这些不同的名称都意味着研究对象的尺寸是微小的,虽然对“微小”的理解存在差异,有人理解为纳米级微小,也有人理解为一个原子的大小。但是,仅就规模缩减而言,并不能很好地描述此类问题的性质。那么,在尺寸缩小后,从力学的角度来看,是什么因素使其加工方法与宏观尺寸不同呢?总之,随着研究对象规模的缩小,表面现象将逐渐占据突出地位。
首先,因为体积缩小,物体的体力与物体的特性有关 尺寸的立方成正比,表面力与尺寸的平方成正比。因此,当研究对象减少时,对象的体力下降得更快。因此,在微观世界中研究的对象都是占据主导地位的表面相关力量。所有的摩擦力、流体阻力和表面张力都是与表面有关的外力,它们将是作用在物体上的主要力。
其次,当研究对象的尺寸减小时,其不均匀性会变得突出。可以看作是均匀多体固体和晶体的粒子脱颖而出,更何况如果再缩小尺寸,就必须考虑原子和分子的作用。流体中的悬浮物也将突出显示。在这种情况下,颗粒之间的界面仍然是必须考虑的最重要的因素,流体与悬浮颗粒之间的相互作用也受表面力的影响。近年来引起人们关注的断裂问题,实用的连续均匀介质法总是得到裂纹尖端应力为无穷大,与实际情况不符。其实这类问题应该从多晶问题的角度来讨论,难免会遇到晶体界面强度的问题。
在研究物体时,无论是动物还是植物,它们的微小单位总会遇到细胞,而细胞就是各种物质包裹在细胞膜中的单位。细胞膜是薄膜,厚度小,表面弯曲。
总之,当我们要处理微观世界的力学现象时,总是要处理各种曲面。
第二、曲面和平行曲面
对于已知曲面r=r(u1,u2),距离z的平行曲面为
其中,n(u1,u2)为曲面的单位法向量。这两个向量线性无关
,所以它们可以作为表面t=r(u1,u2)上的局部坐标系,所以度量二次微分方程与表面是
其中
和平行面rz=(u1,u2)+zn(u1,u2)次微分类型为
这里
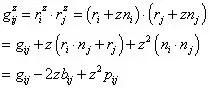
其中H为曲面的平均曲率,K为曲面的高斯曲率。而
也称为曲面的二次二次微分形式,是表征曲面弯曲性质的微分二次形式。二次形式
称为曲面的三次二次微分形式。它是由一阶和二阶微分形式确定的二次型,所以不是一个独立的二次型。
三种或两种算符
由连续介质力学可知,在势力场作用下,力等于势函数的梯度。现在考虑一个势函数 f 在表面 r z 上的梯度。它沿曲面法线方向的梯度比较简单,等于沿法线方向的偏导数。那么问题在于计算曲面 r z 的切平面中的梯度。根据梯度的定义
这里,上标z表示对应的平行面的量。
因为
代入梯度定义公式的g zjk来求解g zij,注意z是一个小量,所以忽略它如果你只保留高级项目一次,你会得到
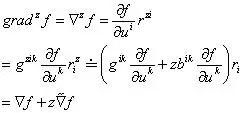
where
这是殷亚军教授在[2, 3]和[4]中介绍的一对算子。这意味着在计算沿平行曲面的梯度时,应沿原始曲面的梯度,加上由于曲面而导致的z的一阶校正。这个修正就是上面提到的算子。
上式是由表征曲面(或几何形状)的几何量bik确定的微分算子。由于表征曲面的几何量不是唯一的,因此这类算子的定义也不是唯一的。 .我们可以将三次二次微分类型的系数pij的表达式写成实体形式:
Furthermore
This It可以看作是关于 b 的二次代数方程。根据吠陀定理,它的两个根满足
类似于b,
也是描述的几何量曲面。尹亚军认为,既然b可以用来定义操作符
那么,
也可以用来定义如下运算符
从上面提到的吠陀定理,我们知道这两个运算符不是独立的。它们满足关系表达式
因此,只需保留这两个运算符之一即可。尹亚军建议保留后者,因为与前者相比,后者具有更高的对称性。最基本的对称是
即两个操作符((如下)
