1. 序言—几则引言

不战而屈人之兵，善之善者也。

——《孙子兵法》

力学家要学会计算，不仅不能卖弄计算，而且要躲避计算。

——周培源

计算机现在不是，也永远不会是解决工程问题的源泉。

——

虽然在结构工程实践中计算机是非常有价值的工具，但是结构工程师必须认识到对工程的细节（即原理，方法，标准，道德等等）的全面了解，比懂得怎样在计算机屏幕上游逛不知要重要多少。警告实际工程师，如果没有计算机他们的结构工程知识不足以胜任工作，他们也没有资格使用计算机（如若不然，那不仅是不道德，而且是犯罪）。

《结构工程师对计算机的滥用》

——《力学与实践》1999年第5期

我原不知道，而且我想任何人也不知道，费米已准备好用一种简单的方法来测量这次爆炸的威力。费米手里握着一把碎纸片，在冲击波来到的时候，我看见他把碎纸片从手中向地面撒去。地面上原没有风，当冲击波袭来时，就把一些碎纸片吹出好几尺远。因为费米已事先量好了撒碎纸片的高度，现在他只需要量一下纸片被风吹开的水平距离。他曾经事先计算过不同爆炸力所应有的各种距离，所以当他量过地面距离之后，很快就说出了这次爆炸的强度。他的测量结果和后来从复杂的仪表上记录下来的数据所作的计算非常接近。

——《现在可以说了》

1911年，我在G?ttingen当助教。当时，Prandtl的主要兴趣在于附面层，这是贴近物体表面的一层流动。Prandtl带了个博士生Karl Hiemenz。他交给后者一个任务，设计一个水槽，使他能观察到圆柱体后面的流动分裂。他的目的是用实验来核对按附面层理论计算出来的分裂点。为此，必须先知道在稳定水流中圆柱体周围的压力强度如何分布。非常出乎Hiemenz的意外，他发现在水槽中的水流不断地发生激烈的摆动。他报告Prandtl，Prandtl告诉他：“显然，你的圆柱体不够圆。”可是，即使圆柱体经过非常细心的加工，结果水流还是继续摆动。于是Prandtl又说，水槽可能不对称。Hiemenz于是又开始调整水槽。

我当时与这个问题并无关系。不过每天早上我进实验室时总问他：“Hiemenz先生，现在流动稳定了没有？”他非常懊丧地回答，“始终在摆动。”这时我想，假使水流始终在摆动，那么这一现象一定有个内在的客观原因。在一个周末，我试计算一下涡系的稳定性。我用非常粗略的方法运算，我假定只有一个涡旋可以自由活动，其他所有涡旋都固定不动。然后让这个涡旋微微移动一些地位，看看计算出来会有什么样的结果。我得到的结论是，如果是对称的排列，那么这个涡旋就一定离开它原来的位置越来越远。对于反对称的排列，虽然也得到同样的结果，但是，当行列的间距和相邻涡旋的间距有一定比值时，这涡旋却停留在它原来位置的附近，并且围绕后者作微小的环形路线运动。第二天我结束了我的计算。在星期一我问Prandtl， “你对这一现象的看法如何？”他回答说，“这里面有些道理，写下来吧，我把你的论文提到学院里去。”

这就是我关于这一问题的第一篇论文。之后，我觉得我的假定有点太武断。我于是又重新研究了一个所有涡旋都能够移动的涡系。这需要稍为复杂一些的数学计算。经过几个星期后计算完毕，我就写出第二篇论文。

——von Karmen《空气动力学的发展》

2. 什么是设计

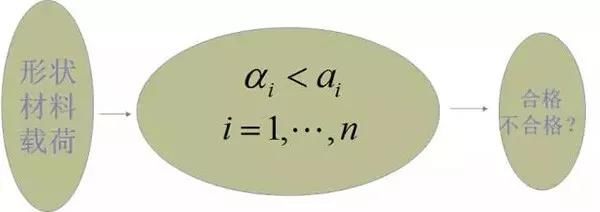
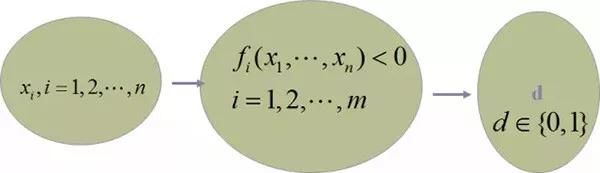
• 原始数据：模糊性，随机性，不确定性。
• 约束：要求无矛盾。
• 输出：是一个布尔量。
• 设计规范：所谓规范实际上就是对设计变量的一系列约束。

好的设计难就难在这些约束有时是模糊的。确定的约束好办，而模糊的约束还是要靠经验来解决。

3. 凭经验设计的例子

雅典女神庙

座落于雅典卫城，建于438B.C.是古希腊建筑的典型例子。

山西应县木塔

建于公元1056年，总高67米，采用双层环形空间结构形式，是现存中国最古老楼阁式木构佛塔。塔建在4米高的两层石砌台基上，内外两排立柱构成双层套筒式结构，柱与柱之间还有大量水平构件，暗层内又有大量斜撑，使双层套筒内外层紧密结合连成一体。其柱不是直接插入地中而是搁置于石础之上。在连接上采用了传统的斗栱结构，为不同部分的特殊需要分别设计了50余种不同形式的斗栱。由于结构上的合理性，近千年间经历了12次6级以上的大地震，迄今安然无恙。